Problem Solving: Difference between revisions
No edit summary |
Monicahanon (talk | contribs) |
||
| (29 intermediate revisions by 3 users not shown) | |||
| Line 26: | Line 26: | ||
===Kirchhoff's Current Law=== | ===Kirchhoff's Current Law=== | ||
[[File:Junction rule.jpeg|500px|thumb|center|Kirchhoff's Current Law]] | |||
We know from Kirchhoff's law that the sum of the currents in each node is zero. This means that the current flowing into the node is the same as the current flowing out of the node. Therefore the multiplication of each column of A by the current vector, y, must be equal to zero: | We know from Kirchhoff's law that the sum of the currents in each node is zero. This means that the current flowing into the node is the same as the current flowing out of the node. Therefore the multiplication of each column of A by the current vector, y, must be equal to zero: | ||
| Line 41: | Line 43: | ||
===Solving Problems=== | ===Solving Problems=== | ||
From Ohm's law we have <math> V = I * R </math>. Thus if we define the conductance | From Ohm's law we have <math> V = I * R </math>. Thus if we define the conductance diagonal matrix <math>C</math> where <math>C_{i,i} = \frac{1}{R_{i}}</math>, <math>C_{i,j} = 0</math>, Ohm's law becomes: | ||
<math>\vec{y} = -CA\vec{x}</math> | <math>\vec{y} = -CA\vec{x}</math> | ||
| Line 48: | Line 50: | ||
<math> -A^{T}CA\vec{x} = f</math> | <math> -A^{T}CA\vec{x} = f</math> | ||
We can now use this system of matrices to solve circuit problems. | |||
It is important to note that for the exercises posted above, the solutions for those problems should be easy to compute given the number of nodes and connections. Nevertheless, bigger and more complex problems would benefit massively from the methods of linear algebra, as they could be computed in this standard way. | |||
==Example== | |||
Suppose we have the following circuit (along with its graph and matrix representation): | |||
[[File:Graph_representation_example.png|600px|thumb|center|Graph representation of a circuit]] | |||
Solving the system, we get: | |||
[[File:Linear_circut_example1.png|500px|thumb|center]] | |||
Notice that <math> C</math> is the identity, thus: | |||
[[File:Linear_circut_example4.png|500px|thumb|center]] | |||
Solving for x, we get the voltages: | |||
[[File:Linear_circut_example5.png|150px|thumb|center]] | |||
= | Finally, we can find the currents using <math>\vec{y} = -CA\vec{x}</math>: | ||
[[File:Linear_circut_example6.png|140px|thumb|center]] | |||
== See also == | == See also == | ||
===Further reading=== | ===Further reading=== | ||
* Linear Algebra applications in image compression: https://math.mit.edu/~gs/linearalgebra/linearalgebra5_7-1.pdf | |||
===External links=== | ===External links=== | ||
Gilbert Strang's "Equilibrium Equations and Minimum Principles": http://cns-web.bu.edu/~eric/EC500/attachments/ON(2d)LINE(20)READINGS/strang.pdf | |||
==References== | ==References== | ||
Latest revision as of 23:28, 29 November 2017
Linear algebra can be used to solve large ohmic circuits. This page explains how to define the circuit problem in terms of a linear system that can be solved with computational methods like matlab or python.
The Main Idea
We can describe an electrical circuit as a graph where the nodes represent specific points and the edges represent the components connecting them. E.g:
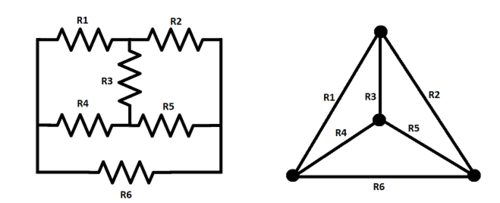
Incidence Matrix
The incidence matrix, A, is a matrix of dimensions m x n, where m is the number of edges and n is the number of nodes. If x is the vector that contains all the nodes in order, A satisfies: [math]\displaystyle{ A\vec{x}_{edge} = x_{end} - x_{start} }[/math] Thus, the resulting matrix will have zeros in every element of each row, except for the start and the end nodes, which will be -1 and 1 respectively:
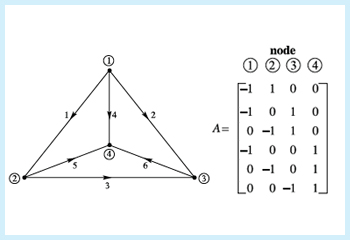
Here, [math]\displaystyle{ x_{1}, x_{2}, x_{3} }[/math] and [math]\displaystyle{ x_{4} }[/math] represent the voltages at the nodes. Then [math]\displaystyle{ A\vec{x}_{edge} = x_{end} - x_{start} }[/math] gives the voltage differences [math]\displaystyle{ ∆V }[/math].
Loop Rule (Kirchhoff's voltage law)
Using this creative way of transforming a circuit to a graph and getting the incidence matrix from it allows us to do some interesting things. Kirchhoff's loop rule is a principle of conservation of energy that implies that the directed sum of the voltage differences around any closed network is zero.
This means that the components of [math]\displaystyle{ A\vec{x} = b }[/math] add to zero around every loop. Moreover, the voltage law can decide whether b is in the column space of A.
We know from Ohm's law that [math]\displaystyle{ V = I * R }[/math]. Then, in the previous graph for example, we would have that [math]\displaystyle{ V_{edge1} = I * R = (direction) * R_{1} = 1 * R_{1} }[/math].
Kirchhoff's Current Law
We know from Kirchhoff's law that the sum of the currents in each node is zero. This means that the current flowing into the node is the same as the current flowing out of the node. Therefore the multiplication of each column of A by the current vector, y, must be equal to zero:
[math]\displaystyle{ A^{T}\vec{y} = 0 }[/math]
where [math]\displaystyle{ y_{i} }[/math] is the current passing through edge [math]\displaystyle{ i }[/math].
If a circuit has a source like a battery, we can treat the entire circuit as a node. The current in and out of every node within the circuit will be zero except for the nodes connected to the positive and negative ends of the battery. For the positive end the net current, [math]\displaystyle{ S }[/math], will be positive and for the negative end the net current will be negative. Thus we get:
[math]\displaystyle{ A^{T}\vec{y} = f }[/math]
where [math]\displaystyle{ f_{i} = 0 }[/math] if [math]\displaystyle{ i }[/math] is not one of the nodes connected to the battery,[math]\displaystyle{ f_{i} = S }[/math] if [math]\displaystyle{ i }[/math] is connected to the positive end and [math]\displaystyle{ f_{i} = -S }[/math] if [math]\displaystyle{ i }[/math] is connected to the negative end.
Solving Problems
From Ohm's law we have [math]\displaystyle{ V = I * R }[/math]. Thus if we define the conductance diagonal matrix [math]\displaystyle{ C }[/math] where [math]\displaystyle{ C_{i,i} = \frac{1}{R_{i}} }[/math], [math]\displaystyle{ C_{i,j} = 0 }[/math], Ohm's law becomes:
[math]\displaystyle{ \vec{y} = -CA\vec{x} }[/math]
where [math]\displaystyle{ y_{i} }[/math] is the current through edge [math]\displaystyle{ i }[/math] and [math]\displaystyle{ x_{j} }[/math] is the voltage at node [math]\displaystyle{ j }[/math] . Substituting for y in Kirchhoff's law, we get:
[math]\displaystyle{ -A^{T}CA\vec{x} = f }[/math]
We can now use this system of matrices to solve circuit problems.
It is important to note that for the exercises posted above, the solutions for those problems should be easy to compute given the number of nodes and connections. Nevertheless, bigger and more complex problems would benefit massively from the methods of linear algebra, as they could be computed in this standard way.
Example
Suppose we have the following circuit (along with its graph and matrix representation):
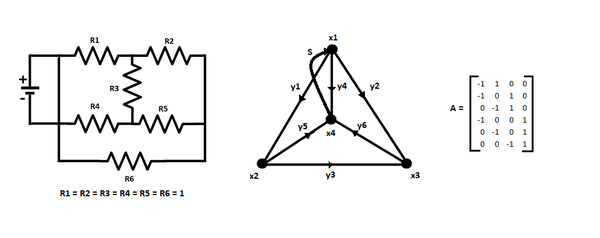
Solving the system, we get:

Notice that [math]\displaystyle{ C }[/math] is the identity, thus:
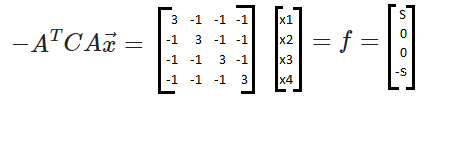
Solving for x, we get the voltages:
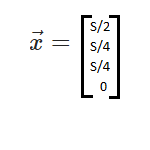
Finally, we can find the currents using [math]\displaystyle{ \vec{y} = -CA\vec{x} }[/math]:
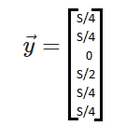
See also
Further reading
- Linear Algebra applications in image compression: https://math.mit.edu/~gs/linearalgebra/linearalgebra5_7-1.pdf
External links
Gilbert Strang's "Equilibrium Equations and Minimum Principles": http://cns-web.bu.edu/~eric/EC500/attachments/ON(2d)LINE(20)READINGS/strang.pdf
References
- Strang, G. (2016), Introduction to Linear Algebra, Wellesley-Cambridge Press, 5th edition, isbn:978-0-9802327-7-6