Potential DIfference Path Independence, claimed by Aditya Mohile: Difference between revisions
Jump to navigation
Jump to search
Kjaworski3 (talk | contribs) |
Kjaworski3 (talk | contribs) No edit summary |
||
| (15 intermediate revisions by the same user not shown) | |||
| Line 1: | Line 1: | ||
== | |||
==Primary Concept== | |||
The voltage between 2 points does not depend on the path taken to travel from one point to another. | The voltage between 2 points does not depend on the path taken to travel from one point to another. | ||
| Line 8: | Line 8: | ||
:<math>\Delta V_{AB}= - \int^B_A \vec{E} \cdot d\vec{l}</math> | :<math>\Delta V_{AB}= - \int^B_A \vec{E} \cdot d\vec{l}</math> | ||
The potential difference from A to B is found by integrating the electric field with respect to the distance between the two points. | The potential difference from A to B is found by integrating the electric field with respect to the distance between the two points. | ||
:<math>\Delta V_{AB}= | :<math>\Delta V_{AB}= {E} \int^B_A d\vec{l}</math> | ||
Here, E is uniform and constant and can be isolated outside of the integral. | |||
===A | :<math>\Delta V_{AB} = {E}\Delta l_{AB}</math> | ||
From this final statement, The potential difference is equivalent to the uniform electric field in the region multiplied by the change in position of the charge from A to B. As a result, it is clear that regardless of the how we get from A to B the only distance that matters is the distance between the final and initial point of the charge acted on. This indicates that the potential difference is "path independent". | |||
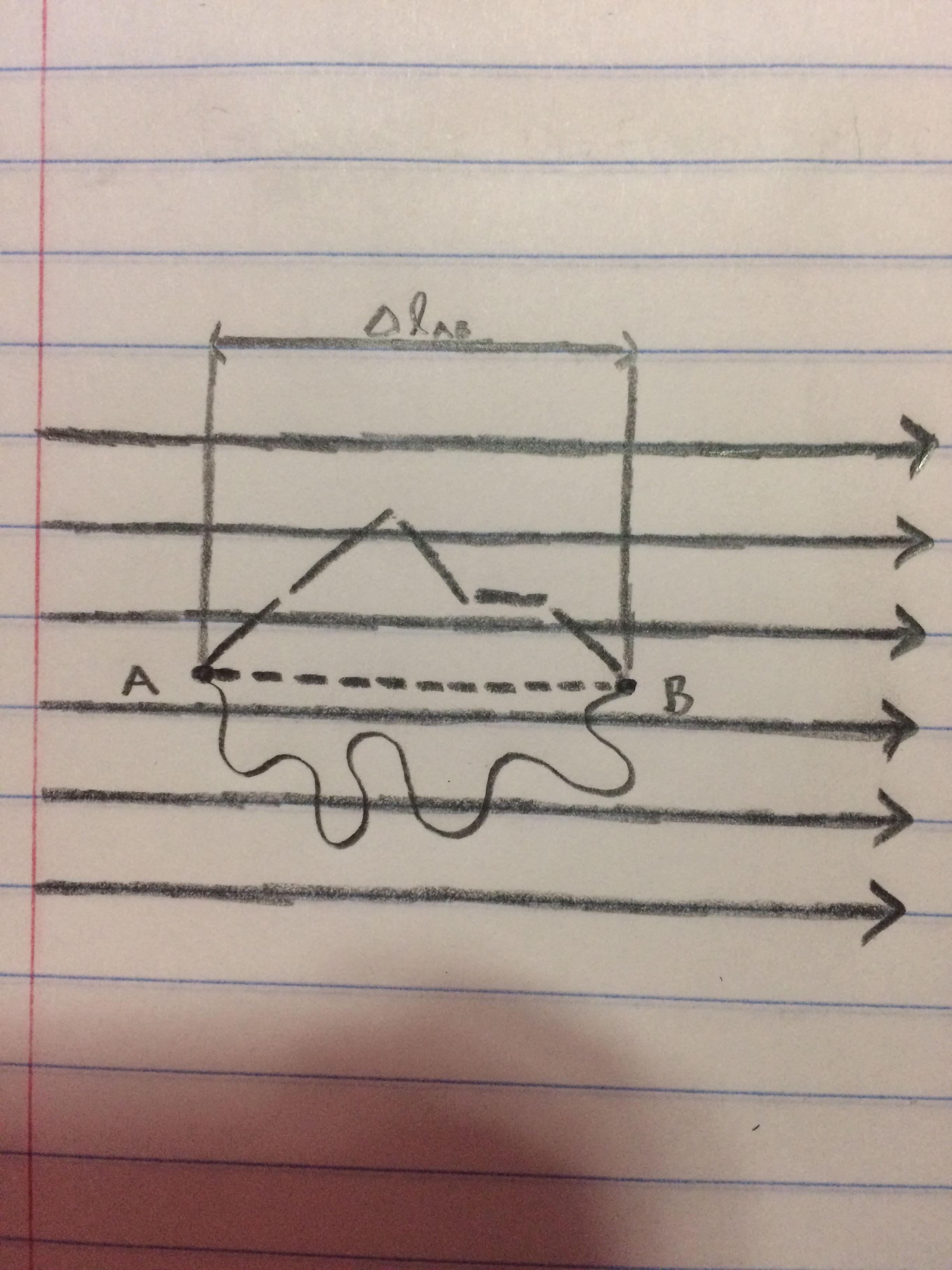
===A Visual Representation=== | |||
[[File:Path_Independence.jpeg]] | |||
==Examples== | ==Examples== | ||
Latest revision as of 20:41, 27 November 2017
Primary Concept
The voltage between 2 points does not depend on the path taken to travel from one point to another.
A Mathematical Understanding
- [math]\displaystyle{ \Delta V_{AB}= - \int^B_A \vec{E} \cdot d\vec{l} }[/math]
The potential difference from A to B is found by integrating the electric field with respect to the distance between the two points.
- [math]\displaystyle{ \Delta V_{AB}= {E} \int^B_A d\vec{l} }[/math]
Here, E is uniform and constant and can be isolated outside of the integral.
- [math]\displaystyle{ \Delta V_{AB} = {E}\Delta l_{AB} }[/math]
From this final statement, The potential difference is equivalent to the uniform electric field in the region multiplied by the change in position of the charge from A to B. As a result, it is clear that regardless of the how we get from A to B the only distance that matters is the distance between the final and initial point of the charge acted on. This indicates that the potential difference is "path independent".