Snell's Law: Difference between revisions

Latest revision as of 23:21, 5 December 2015

Snell's Law (also known as the Snell-Descartes Law and the Law of Refraction) describes the relationship between angles of incidence and refraction for a wave impinging on an interface between two different mediums with correlating indices of refraction. We derive this formula from the bending of light waves and the speed of wavefronts in two different media. In short, describing the relationship between the angles and velocities of waves.

Error creating thumbnail: sh: /usr/bin/convert: No such file or directory Error code: 127

Snell's Law Outlook

History

Although, named after the Dutch astronomer Willebrord Snellis (1580-1626), the law was first accurately depicted by Ibn Sahl (c. 940-1000). Sahl was a Muslim physicist of Baghdad who made us of it to work out different shapes of lenses that were able to focus light with no geometric aberrations, known as anaclastic lenses. In later years, the law was rediscovered by Thomas Harriot in 1602, although not published derived a similiar mathematically equivalent form, which remained unpublished during his lifetime. In French, Snell's Law is called "la loi de Descartes" or "loi de Snell-Descartes."

A Mathematical Model

Snell's Law equals the ratio of material velocities V1 and V2 to the sine's of incident (Q1) and refracted (Q2) angles.

[math]\displaystyle{ \frac{\sin\theta_1}{\sin\theta_2} = \frac{v_1}{v_2} = \frac{\lambda_1}{\lambda_2} = \frac{n_2}{n_1} }[/math]

To manipulate this equation:

[math]\displaystyle{ {n_1\sin\theta_1} = {n_2\sin\theta_2} }[/math]

Where n1 and n2 are the indices of refraction of the two media and the degrees(thetas) are the angles the incident and transmitted rays , respectively, take on with their normal state.

Examples

A beam of light travels through water and hits a glass surface. The angle between the incident beam and the normal to the glass surface is 23 degrees. The index of refraction of water is 1.33 and the index of refraction of this type of glass is 1.65. What is the refracted angle?

Error creating thumbnail: sh: /usr/bin/convert: No such file or directory Error code: 127

[math]\displaystyle{ {n_1\sin\theta_1} = {n_2\sin\theta_2} }[/math]

[math]\displaystyle{ {\sin\theta_2} = \frac{n_1\sin\theta_1}{n_2} }[/math]

[math]\displaystyle{ {\theta_2} = arcsin\frac{1.33\sin23}{1.65}= 18.4 degrees }[/math]

Connectedness

Snell's Law plays a large role in understanding refraction and the basic topic of light traveling through different media and forums. Although not studied on our final exam, we can still utilize this topic and idea to understand the wavelike movement of light, known as the movement of electromagnetic radiation.

@@ Line 1: / Line 1: @@
-==Snell's Law==
 Snell's Law (also known as the Snell-Descartes Law and the Law of Refraction) describes the relationship between angles of incidence and refraction for a wave impinging on an interface between two different mediums with correlating indices of refraction. We derive this formula from the bending of light waves and the speed of wavefronts in two different media. In short, describing the relationship between the angles and velocities of waves.
-===A Mathematical Model===
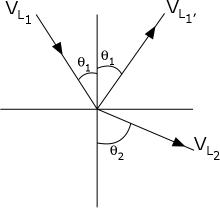
+[[File:SnellsLawAngles1.png|thumb|right|Snell's Law Outlook]]
- Snell's Law equals the ratio of material velocities V1 and V2 to the sine's of incident (Q1) and refracted (Q2) angles.
+===History===
+Although, named after the Dutch astronomer Willebrord Snellis (1580-1626), the law was first accurately depicted by Ibn Sahl (c. 940-1000). Sahl was a Muslim physicist of Baghdad who made us of it to work out different shapes of lenses that were able to focus light with no geometric aberrations, known as anaclastic lenses. In later years, the law was rediscovered by Thomas Harriot in 1602, although not published derived a similiar mathematically equivalent form, which remained unpublished during his lifetime.  In French, Snell's Law is called "la loi de Descartes" or "loi de Snell-Descartes."
+===A Mathematical Model===
+ Snell's Law equals the ratio of material velocities V1 and V2 to the sine's of incident (Q1) and refracted (Q2) angles.
-====A Computational Model====
+[[File:Snells_Law.jpeg]]
-How do we visualize or predict using this topic. Consider embedding some vpython code here [https://trinket.io/glowscript/31d0f9ad9e Teach hands-on with GlowScript]
+:<math>\frac{\sin\theta_1}{\sin\theta_2} = \frac{v_1}{v_2} = \frac{\lambda_1}{\lambda_2} = \frac{n_2}{n_1}</math>
-===First Law===
-The first law of thermodynamics defines the internal energy (E) as equal to the difference between heat transfer (Q) ''into'' a system and work (W) ''done by'' the system.  Heat removed from a system would be given a negative sign and heat applied to the system would be given a positive sign.  Internal energy can be converted into other types of energy because it acts like potential energy.  Heat and work, however, cannot be stored or conserved independently because they depend on the process.  This allows for many different possible states of a system to exist.  There can be a process known as the adiabatic process in which there is no heat transfer.  This occurs when a system is full insulated from the outside environment.  The implementation of this law also brings about another useful state variable, '''enthalpy'''.
+To manipulate this equation:
-====A Mathematical Model====
-E2 - E1 = Q - W
+:<math>{n_1\sin\theta_1} =  {n_2\sin\theta_2}</math>
-==Second Law==
+Where n1 and n2 are the indices of refraction of the two media and the degrees(thetas) are the angles the incident and transmitted rays , respectively, take on with their normal state.
-The second law states that there is another useful variable of heat, entropy (S).  Entropy can be described as the disorder or chaos of a system, but in physics, we will just refer to it as another variable like enthalpy or temperature.  For any given physical process, the combined entropy of a system and the environment remains a constant if the process can be reversed.  The second law also states that if the physical process is irreversible, the combined entropy of the system and the environment must increase.  Therefore, the final entropy must be greater than the initial entropy.
+===Examples===
-===Mathematical Models===
+A beam of light travels through water and hits a glass surface. The angle between the incident beam and the normal to the glass surface is 23 degrees. The index of refraction of water is 1.33 and the index of refraction of this type of glass is 1.65. What is the refracted angle?
-delta S = delta Q/T
+[[File:ExampleProb1.jpg|thumb|right]]
-Sf = Si (reversible process)
-Sf > Si (irreversible process)
-===Examples===
+:<math>{n_1\sin\theta_1} =  {n_2\sin\theta_2}</math>
-'''Reversible process''': Ideally forcing a flow through a constricted pipe, where there are no boundary layers. As the flow moves through the constriction, the pressure, volume and temperature change, but they return to their normal values once they hit the downstream.  This return to the variables' original values allows there to be no change in entropy.  It is often known as an isentropic process.
+:<math>{\sin\theta_2} = \frac{n_1\sin\theta_1}{n_2}</math>
-'''Irreversible process''': When a hot object and cold object are put in contact with each other, eventually the heat from the hot object will transfer to the cold object and the two will reach the same temperature and stay constant at that temperature, reaching equilibrium.  However, once those objects are separated, they will remain at that equilibrium temperature until something else acts upon it.  The objects do not go back to their original temperatures so there is a change in entropy.
+:<math> {\theta_2} = arcsin\frac{1.33\sin23}{1.65}= 18.4  degrees </math>
-==Connectedness==
+===Connectedness===
-#How is this topic connected to something that you are interested in?
-#How is it connected to your major?
-#Is there an interesting industrial application?
-==History==
+Snell's Law plays a large role in understanding refraction and the basic topic of light traveling through different media and forums. Although not studied on our final exam, we can still utilize this topic and idea to understand the wavelike movement of light, known as the movement of electromagnetic radiation.
-Thermodynamics was brought up as a science in the 18th and 19th centuries.  However, it was first brought up by Galilei, who introduced the concept of temperature and invented the first thermometer.  G. Black first introduced the word 'thermodynamics'.  Later, G. Wilke introduced another unit of measurement known as the calorie that measures heat.   The idea of thermodynamics was brought up by Nicolas Leonard Sadi Carnot.  He is often known as "the father of thermodynamics".  It all began with the development of the steam engine during the Industrial Revolution.  He devised an ideal cycle of operation.  During his observations and experimentations, he had the incorrect notion that heat is conserved, however he was able to lay down theorems that led to the development of thermodynamics.  In the 20th century, the science of thermodynamics became a conventional term and a basic division of physics.  Thermodynamics dealt with the study of general properties of physical systems under equilibrium and the conditions necessary to obtain equilibrium.
 == See also ==
-Are there related topics or categories in this wiki resource for the curious reader to explore?  How does this topic fit into that context?
+http://www.physicsbook.gatech.edu/Lenses
+http://www.physicsbook.gatech.edu/Light_Refraction:_Bending_of_light
 ===Further reading===
-Books, Articles or other print media on this topic
+Matter & Interactions, Vol. II: Electric and Magnetic Interactions, 4nd Edition by R. Chabay & B. Sherwood (John Wiley & Sons 2015)
+https://www.math.ubc.ca/~cass/courses/m309-01a/chu/Fundamentals/snell.htm
 ===External links===
-Internet resources on this topic
+http://www.physicsclassroom.com/class/refrn/Lesson-2/Snell-s-Law
+https://en.wikipedia.org/wiki/Snell's_law
 ==References==
-https://www.grc.nasa.gov/www/k-12/airplane/thermo0.html
+Matter & Interactions, Vol. II: Electric and Magnetic Interactions, 4nd Edition by R. Chabay & B. Sherwood (John Wiley & Sons 2015)
-http://hyperphysics.phy-astr.gsu.edu/hbase/thermo/thereq.html
-https://www.grc.nasa.gov/www/k-12/airplane/thermo2.html
+http://hyperphysics.phy-astr.gsu.edu/hbase/geoopt/refr.html
-http://www.phys.nthu.edu.tw/~thschang/notes/GP21.pdf
-http://www.eoearth.org/view/article/153532/
-[[Category:Which Category did you place this in?]]
+[[Category:Radiation]]

Snell's Law: Difference between revisions

Latest revision as of 23:21, 5 December 2015

Contents

History

A Mathematical Model

Examples

Connectedness

See also

Further reading

External links

References

Navigation menu