Real Systems
This page describes real systems and how they can be used to model certain aspects of a system's motion.
The Main Idea
A real system is a system in which every part of the system is modeled separately, allowing for the internal behaviors of the system to be analyzed in addition to the system's motion through its environment.
In Point Particle Systems, forces are analyzed as though they act directly on the system's center of mass, and only the translational kinetic energy of a system can change. Through week 9, we have been most bodies as point particles, as we have been primarily interested in their translational motion. However, we may now encounter problems where we want to analyze the internal behaviors of systems as well. For example, we may want to calculate a change in a system's Translational, Rotational and Vibrational Energy, Potential Energy, or Thermal Energy. In a real system, the point of application of each force must be considered. Furthermore, when calculating the work done by a force, the distance over which the force is applied is not the distance traveled by the system's center of mass, but rather the distance traveled by the force's point of contact. These two key differences lead to a mathematical model that can be more complicated than that of a point particle system, but yields insights about the internal behavior of the system.
A Mathematical Model
The mathematical concepts used to analyze point particle systems depend on the system. Often, the work-energy theorem (see Work/Energy) is used. This section explains how to use the work-energy theorem for a point particle system because this is the concept that varies the most significantly from its application to point particle systems.
The work done on a real system should be calculated separately for each force acting on it because each force might be exerted over a different distance due to the geometry of the system. The work done on a real system by each force is defined as
[math]\displaystyle{ W = \int \vec{f} \cdot d \vec{r} }[/math],
where [math]\displaystyle{ \vec{r} }[/math] is the position of the point on the system on which the force acts.
Let us assume that the force acting on the system is constant, so that we can get rid of the integral, and that the force acts in the direction of the system's motion, so that we can replace the dot product with regular multiplication. This will be the case for most real system problems involving work. With these assumptions, the work done on a part of a real system by a force is given by
[math]\displaystyle{ W = f * d }[/math]
where [math]\displaystyle{ F_{net} }[/math] is the magnitude of the net force acting on the particle and [math]\displaystyle{ d }[/math] is the distance over which the force is exerted. For real systems, that is the distance traveled by the point of contact of the force, which may not be the same as the distance traveled by the system's center of mass, depending on the movement of the systems' different parts. This contrasts with point particle systems, where the distance over which the force is exerted is simply the displacement of the system's center of mass.
The work-energy theorem states that work done on a system increases that system's energy. For real systems, this is the system's total energy. Since each force's work must be found separately in a real system, remember to sum the values of the work done by the different forces acting on the system.
In other words, for a real system,
[math]\displaystyle{ \Delta E = \sum_i f_i * d_i }[/math].
The equation above is the basis for answering work/energy questions using real systems. It is important to remember that when modeling a system as a real system, calculating the work done on the system as described above finds all of the work done on the system- both translational kinetic energy and internal types of energy.
A Computational Model
Most computer simulations treat systems as real systems, modeling each part of a system separately. This is because Iterative Prediction makes keeping track of each part of the system separately easy even when it might be difficult to do so analytically. The last example on the Point Particle Systems page describes a system in which two masses are connected by a spring and one of them is pulled by a force. Consider the following simulation of the system:
If you click "view source" on the top left corner, you will see that the process of iterative prediction is performed separately for each of the two masses- they each have their own position vectors, and the forces acting on each are calculated. There is no need to treat them as a single particle and thereby lose information about their internal behavior- in this case, their oscillations.
Examples
Some of the examples on the Point Particle Systems page can also be analyzed as real systems. Modeling each system as a real system makes the math more complicated but allows us to calculate the internal energies of the systems. Let us look at each example from the point particle systems page.
1.
A 60kg person jumps straight up in the air from a crouching position. From the time the person begins to push off of the ground to the time their feet leave the ground, their center of mass moves up 2m, and the normal force between the ground and the person's feet has a constant magnitude of twice the person's weight. Find the velocity of the jumper at the moment their feet leave the ground. Use 10m/s2 for g.
In this problem, the internal energy of the person does not change, so modeling the jumper as a real system offers few advantages. In fact, it makes it difficult to take an energy approach to answer the question, since when the person is modeled as a real system, the point of contact of the normal force does not move and so does not do work. Instead, forces in the person's legs do work, but the amount of work they do is difficult to calculate since different parts of the legs move different amounts. This problem is best analyzed as a point particle system.
2.
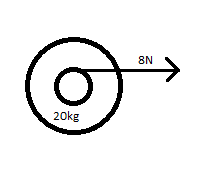
A giant 20kg yo-yo floats at rest in space. Its string (whose mass is negligible compared to the mass of the yo-yo) is pulled with a constant force of 8N. What is the speed of the yo-yo when it has travelled 5m?
This problem can be analyzed as a real system, although it requires knowledge of rotational physics and is more difficult than treating it like a point particle.
The work done on the yo-yo is no longer simply 40Nm because the point of the force's application travels faster than the yo-yo's center of mass due to the yo-yo's rotation. Let us find the distance over which the force is exerted.
Because the force applies a constant torque, the yo-yo undergoes constant angular acceleration [math]\displaystyle{ \alpha }[/math]. Let us say it takes [math]\displaystyle{ t_1 }[/math] seconds for the yo-yo to travel the 5m. The average angular velocity of the yo-yo over that time period is
[math]\displaystyle{ \omega_{avg} = \frac{1}{2} \alpha t_1 }[/math].
This means that the distance traveled by the point of contact between the yo-yo and the string due to the yo-yo's rotation during the [math]\displaystyle{ t_1 }[/math]-second interval is given by
[math]\displaystyle{ d_{rot} = \frac{1}{2} \alpha {t_1}^2 r }[/math],
where r is the radius of the yo-yo (the radius of the string wrapping around it, not the radius of its outer rim).
The total work done on the yo-yo is given by
[math]\displaystyle{ W = f * (d_{trans} + d_{rot}) }[/math]
[math]\displaystyle{ W = f * (d_{trans} + \frac{1}{2} \alpha {t_1}^2 r) }[/math] (d_{trans} is the 5m traveled by the yo-yo's center of mass).
Let us manipulate this expression. Let us start by distributing out the force at the beginning:
[math]\displaystyle{ W = f * d_{trans} + f * \frac{1}{2} \alpha {t_1}^2 r }[/math].
The second term has both f and r as factors. Since the product of these two is the torque exerted by the force, we can replace [math]\displaystyle{ f*r }[/math] with [math]\displaystyle{ T }[/math] for torque:
[math]\displaystyle{ W = f * d_{trans} + \frac{1}{2} \alpha {t_1}^2 T }[/math].
Next, since [math]\displaystyle{ T = I\alpha }[/math] for fixed-plane rotations, we can replace [math]\displaystyle{ T }[/math] with [math]\displaystyle{ I\alpha }[/math], where [math]\displaystyle{ I }[/math] is the moment of inertia of the yo-yo:
[math]\displaystyle{ W = f * d_{trans} + \frac{1}{2} \alpha^2 {t_1}^2 I }[/math].
Finally, we can replace the product [math]\displaystyle{ \alpha * t_1 }[/math] with [math]\displaystyle{ \omega_1 }[/math], the angular velocity of the yo-yo when it reaches the 5m mark:
[math]\displaystyle{ W = f * d_{trans} + \frac{1}{2} {\omega_1}^2 I }[/math].
This expression is the amount of work done on the yo-yo, and since its initial energy of the yo-yo is 0, this expression also gives the final total energy of the yo-yo. Some of it is translational kinetic energy, and some of it is rotational kinetic energy. We recognize the expression [math]\displaystyle{ \frac{1}{2} I {\omega_1}^2 }[/math] as the final rotational kinetic energy of the yo-yo, so that leaves [math]\displaystyle{ f * d_{trans} }[/math] as the final translational kinetic energy of the yo-yo. This is 8 * 5 = 40 Joules, which is the same for the final translational kinetic energy of the yo-yo that we got on the Point Particle Systems page, from which the yo-yo's translational speed can be easily calculated.
As you can see, we were able to save a lot of work by treating the yo-yo as a point particle system.
Connectedness
How is this topic connected to something that you are interested in?
This topic interests me because from one single system you can mathematically determine the other forms of energy that can occur in various physical interaction. From the other forms of energy, you can determine whether there is enough energy to maybe change the temperature of another substance via thermal energy or even change the substance that is in the system given a big enough change in chemical energy.
How is it connected to your major?
As a chemical engineering major, the application of Real Systems is largely used for the majority of mathematics in my major dealing with energy balances. From only analyzing a system from a point particle method, one would only be able to find the change in the translational kinetic energy. In my major, it is very important to consider the entire system in order to find important values such as the change in thermal and kinetic energy because these values are often associated with the amount of work and heat produced in many chemical engineering processes.
Is there an interesting industrial application?
There is an absolute overload of interesting industrial applications for the analysis of real systems. In fact, the analysis of real systems in terms of energy balances is the entirety of what I've done in my chemical engineering classes thus far (I am currently a second year). There are many interesting (depending on your taste) uses of the real system analysis on a multitude of different turbines and chemical reactors.
See also
Further reading
http://p3server.pa.msu.edu/coursewiki/doku.php?id=183_notes:pp_vs_real
External links
References
Chabay, Ruth W., and Bruce A. Sherwood. "9." Matter & Interactions. N.p.: n.p., n.d. N. pag. Print.
Wiki Commons Picture
--Nfortingo3(talk) 19:26, 28 November 2015 (EST)