Electromagnetic Propagation: Difference between revisions
No edit summary |
No edit summary |
||
| (12 intermediate revisions by the same user not shown) | |||
| Line 1: | Line 1: | ||
Electromagnetic Propagation Model | Electromagnetic Propagation Model | ||
BY CHIAGOZIEM OBI | |||
==The Main Idea== | ==The Main Idea== | ||
| Line 8: | Line 9: | ||
===Gauss's Law for Electricity and Magnetism=== | ===Gauss's Law for Electricity and Magnetism=== | ||
<math>\sum \phi_{electric} = \frac{q_{inside}}{\epsilon_0} = \int </math> | <math>\sum \phi_{electric} = \frac{q_{inside}}{\epsilon_0} = \int \vec{E} \bullet d\vec{A} </math> | ||
<math>\sum \phi_{magnetic} = 0</math> | <math>\sum \phi_{magnetic} = 0 = \int \vec{B} \bullet d\vec{A} </math> | ||
===Faraday's Law=== | ===Faraday's Law=== | ||
<math> | <math> \int \vec{E} \bullet d\vec{l} = -\frac{d\phi_{magnetic}}{dt}</math> | ||
===Ampere-Maxwell Law=== | |||
<math> \int \vec{B} \bullet d\vec{l} = \mu_0\epsilon_0\frac{d\phi_{electric}}{dt} + \mu_0I_{enclosed}</math> | |||
== | ==An Interactive Computational Model== | ||
Follow this link to find an interesting little animation. | |||
http://www.walter-fendt.de/ph14e/emwave.htm | |||
== | ==Proposed Model== | ||
Waves may be a familiar concept. We can imagine waves as the familiar up-and-down movement of crests and troughs. The concept of a wave is also applicable to the physics of radiation. According to Maxwell’s equations, a time varying electric field produces a magnetic field, just as a time varying electric field produces a magnetic field. We can try to picture what such a time varying field would “look” like. Let’s propose a model for it. | Waves may be a familiar concept. We can imagine waves as the familiar up-and-down movement of crests and troughs. The concept of a wave is also applicable to the physics of radiation. According to Maxwell’s equations, a time varying electric field produces a magnetic field, just as a time varying electric field produces a magnetic field. We can try to picture what such a time varying field would “look” like. Let’s propose a model for it. | ||
| Line 34: | Line 33: | ||
=== | ===Does the Model Fit the Math?=== | ||
===Gauss's Law=== | ===Gauss's Law=== | ||
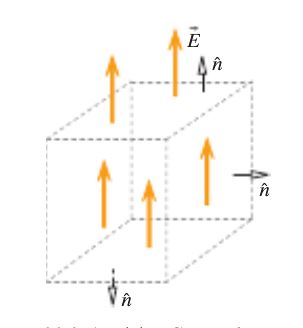
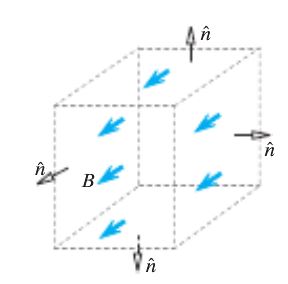
Lets use the slab as a Gauss surface. Calculate the flux through the surface. Applying Gauss' Law shows us that since there is equal amounts of magnetic and electric flux going into and out of the slab, there is no net charge or magnetic monopole through the slab. | |||
[[File:Gauss Electric.JPG]] | |||
[[File:Gauss_Magnetic.JPG]] | |||
===Faraday's Law=== | ===Faraday's Law=== | ||
| Line 45: | Line 46: | ||
===Ampere-Maxwell Law=== | ===Ampere-Maxwell Law=== | ||
This law states that the magnetic field times the path length is equal to | [[File:Amperepath.JPG ]] | ||
So using our model of a box-like particle and applying Maxwell’s equations to it, we’ve found that E = vB and B = | This law states that the magnetic field times the path length is equal to <math>\mu_0 \sum I_{enclosed}+ \frac{d\phi_{electric}}{dt}\mu_0\epsilon_0</math> The change in electric flux is equal to Evh. The magnetic field integral is Bh. Equating the two yields that <math>\mu_0\epsilon_0Evh = Bh </math> Simplifying yields that <math> B = \mu_0\epsilon_0vE</math> | ||
So using our model of a box-like particle and applying Ampere-Maxwell’s equations to it, we’ve found that <math> E = vB </math> and <math> B = \mu_0\epsilon_0vE </math> Also the electric flux and magnetic flux equal zero. Solving for v we find that v = 3e8 m/s. This is the speed of light. | |||
==Connectedness== | |||
This model of electromagnetic waves allows us to predict the effects of light and other waves on matter. We know that light can be polarized into one direction, which is practical for use in optics. We also can determine the interaction between these waves and charged particles. For instance, one important idea is that electromagnetic waves carry energy. Chemists use the properties of light energy in techniques called spectroscopy. Magnetic and electric waves and fields are critical in determining structure of unknown molecules. | |||
=== | ===History of Application=== | ||
One historical application is Nuclear magnetic resonance (NMR) imaging of chemical substances to determine structure. A sample is exposed to powerful magnetic fields, in order to align the particles. Magnetic spins of the electrons of the Hydrogen atoms. They align in the most favorable (lowest energy) alignment. Then the sample is blasting with varying frequencies of electric field (up to 300million Hz) and the frequency at which the electrons move out of alignment is recorded. This information is then used to determine structures of molecules. (Can you tell that I'm a biochem major?) | |||
The application of this method stems from the understanding of how these waves interact with the charged particles of matter. Our models for atoms and electromagnetic waves allow us to make useful and accurate predictions about chemical structure. It is also a great tool for stressing out aspiring biochem majors. (Reading NMR graphs is very difficult. Google it. You'll see what I mean.) | |||
== See also == | == See also == | ||
[http://www.physicsbook.gatech.edu/Light_Scaterring:_Why_is_the_Sky_Blue Why is the Sky Blue] | |||
===Further reading=== | ===Further reading=== | ||
Matter and Interactions Textbook (Section 23.2) | |||
===External links=== | ===External links=== | ||
[https://www.youtube.com/watch?v=4CtnUETLIFs Quick Animation] | |||
[https://www.youtube.com/watch?v=d50avTf0OLw Tutor Literally Yelling Information at You (JK his voice is just loud)] | |||
[http://imagine.gsfc.nasa.gov/science/toolbox/emspectrum1.html NASA on Electromagnetic Waves] | |||
==References== | ==References== | ||
Matter and Interactions Textbook Section 23.2 | |||
[[Category: | [[Category:Radiation]] | ||
Edited by Chiagoziem Obi | Edited by Chiagoziem Obi | ||
Latest revision as of 22:23, 2 December 2015
Electromagnetic Propagation Model BY CHIAGOZIEM OBI
The Main Idea
What is the ideal model for the propagation of electromagnetic waves? Does it look like a sheet of electrons? Maybe it can be described as a spring? A mountain? No! The following explains why the best model is a traveling slab of perpendicular waves that oscillate back and forth.
A Mathematical Model: Maxwell's Equations
Gauss's Law for Electricity and Magnetism
[math]\displaystyle{ \sum \phi_{electric} = \frac{q_{inside}}{\epsilon_0} = \int \vec{E} \bullet d\vec{A} }[/math] [math]\displaystyle{ \sum \phi_{magnetic} = 0 = \int \vec{B} \bullet d\vec{A} }[/math]
Faraday's Law
[math]\displaystyle{ \int \vec{E} \bullet d\vec{l} = -\frac{d\phi_{magnetic}}{dt} }[/math]
Ampere-Maxwell Law
[math]\displaystyle{ \int \vec{B} \bullet d\vec{l} = \mu_0\epsilon_0\frac{d\phi_{electric}}{dt} + \mu_0I_{enclosed} }[/math]
An Interactive Computational Model
Follow this link to find an interesting little animation.
http://www.walter-fendt.de/ph14e/emwave.htm
Proposed Model
Waves may be a familiar concept. We can imagine waves as the familiar up-and-down movement of crests and troughs. The concept of a wave is also applicable to the physics of radiation. According to Maxwell’s equations, a time varying electric field produces a magnetic field, just as a time varying electric field produces a magnetic field. We can try to picture what such a time varying field would “look” like. Let’s propose a model for it.
We can call this single traveling box of field a pulse. There are no charges inside or outside of it. It is simply a traveling box of electric field. It generates a perpendicular magnetic field. Both electric field and magnetic field are perpendicular to the direction that the fields are moving. We can call this a “pulse” of electromagnetic field.
In order to be an acceptable model, it must satisfy all four of the equations of Maxwell. Applying Guass’s law for electricity and magnetism we see that the model works out.
Does the Model Fit the Math?
Gauss's Law
Lets use the slab as a Gauss surface. Calculate the flux through the surface. Applying Gauss' Law shows us that since there is equal amounts of magnetic and electric flux going into and out of the slab, there is no net charge or magnetic monopole through the slab.
Faraday's Law
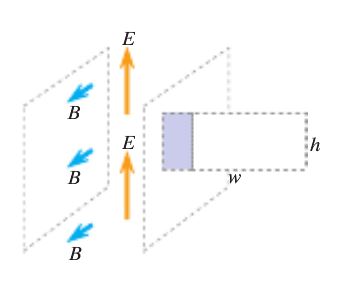
Applying Faraday’s law involves realizing that the pulse in moving through space, and, for an imaginary path, the flux is changing through that path. We can pick a path h high and w wide, and allow part of the path to be inside the box of pulse and some of the path to be outside the pulse, initially. A short time, Δt, later the pulse has moved, encompassing more of the path. The change in the flux is the magnitude of the magnetic field times the velocity of the particle times the height of the path. The change in flux is equal to the emf around the path. The electric field times the height is equal to the emf. So Eh = Bvh. Simplifying that solution yields that the electric field is equal to the velocity times the magnetic field.
Ampere-Maxwell Law
This law states that the magnetic field times the path length is equal to [math]\displaystyle{ \mu_0 \sum I_{enclosed}+ \frac{d\phi_{electric}}{dt}\mu_0\epsilon_0 }[/math] The change in electric flux is equal to Evh. The magnetic field integral is Bh. Equating the two yields that [math]\displaystyle{ \mu_0\epsilon_0Evh = Bh }[/math] Simplifying yields that [math]\displaystyle{ B = \mu_0\epsilon_0vE }[/math]
So using our model of a box-like particle and applying Ampere-Maxwell’s equations to it, we’ve found that [math]\displaystyle{ E = vB }[/math] and [math]\displaystyle{ B = \mu_0\epsilon_0vE }[/math] Also the electric flux and magnetic flux equal zero. Solving for v we find that v = 3e8 m/s. This is the speed of light.
Connectedness
This model of electromagnetic waves allows us to predict the effects of light and other waves on matter. We know that light can be polarized into one direction, which is practical for use in optics. We also can determine the interaction between these waves and charged particles. For instance, one important idea is that electromagnetic waves carry energy. Chemists use the properties of light energy in techniques called spectroscopy. Magnetic and electric waves and fields are critical in determining structure of unknown molecules.
History of Application
One historical application is Nuclear magnetic resonance (NMR) imaging of chemical substances to determine structure. A sample is exposed to powerful magnetic fields, in order to align the particles. Magnetic spins of the electrons of the Hydrogen atoms. They align in the most favorable (lowest energy) alignment. Then the sample is blasting with varying frequencies of electric field (up to 300million Hz) and the frequency at which the electrons move out of alignment is recorded. This information is then used to determine structures of molecules. (Can you tell that I'm a biochem major?)
The application of this method stems from the understanding of how these waves interact with the charged particles of matter. Our models for atoms and electromagnetic waves allow us to make useful and accurate predictions about chemical structure. It is also a great tool for stressing out aspiring biochem majors. (Reading NMR graphs is very difficult. Google it. You'll see what I mean.)
See also
Further reading
Matter and Interactions Textbook (Section 23.2)
External links
Tutor Literally Yelling Information at You (JK his voice is just loud)
References
Matter and Interactions Textbook Section 23.2
Edited by Chiagoziem Obi